橢圓規

• 相關頁面 - 畫橢圓機構

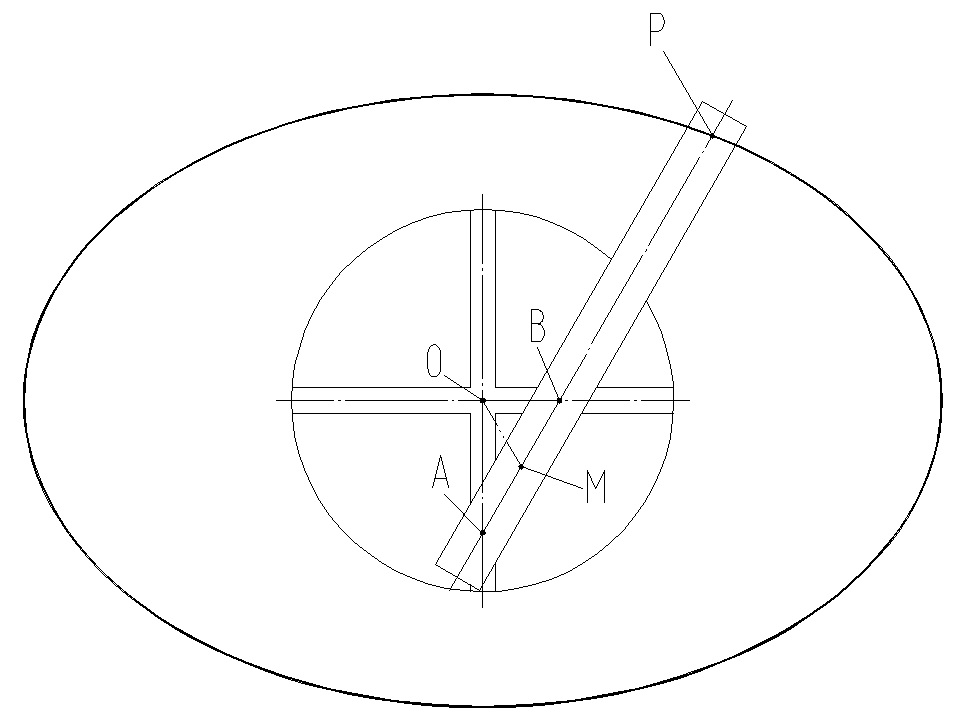
A、B 為滑塊位置，M 為 AB 之中點，曲柄為 OM，連桿為 MA、MB，由三角形 OAB 可知 M 為外心，外心到三端點等距，所以 $OM=MA=MB$（曲柄長度等於連桿長度），且 OM 在橢圓規轉動時距離不變，運動軌跡為一圓。

若以順時鐘而言，A 滑塊將會向上邊滑動，B 滑塊向右滑動，P 點則會逐漸向橢圓右邊的長軸頂點移動，當 A 點和 O 點重合時，P 點正好會和右邊長軸頂點重合。

繼續轉動 A 仍然向上滑動，B 則變為向左滑動，P 點會逐漸靠向橢圓下方的短軸頂點，當 B 點和 O 點重合時，P 點會正好與下方短軸頂點重合。以此類推，持續轉動則可畫出一個橢圓。

橢圓公式

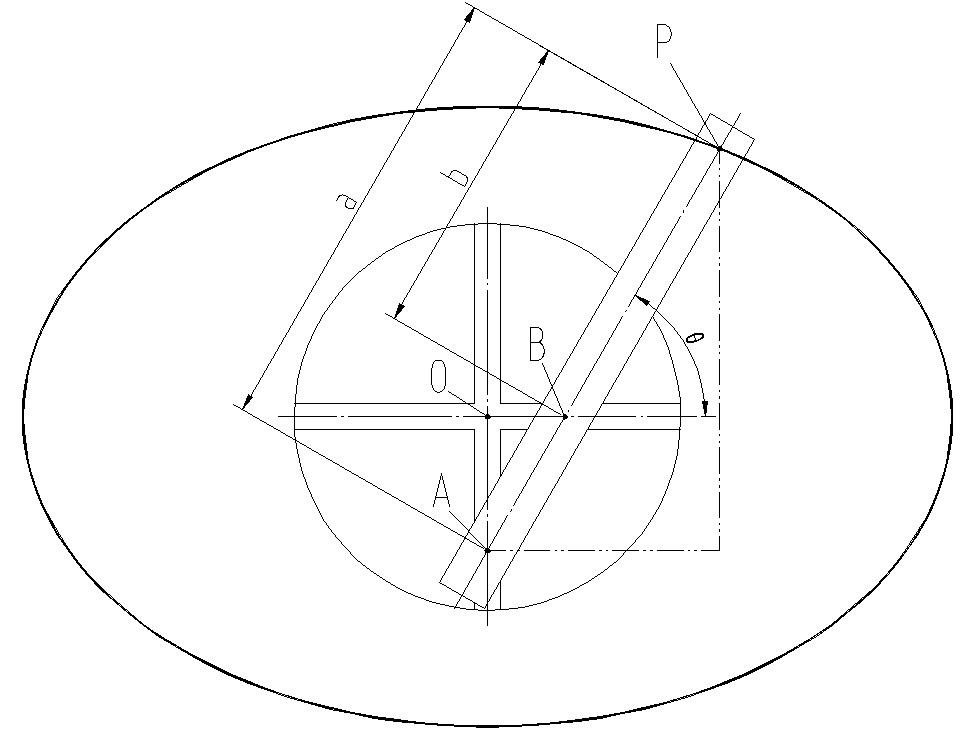
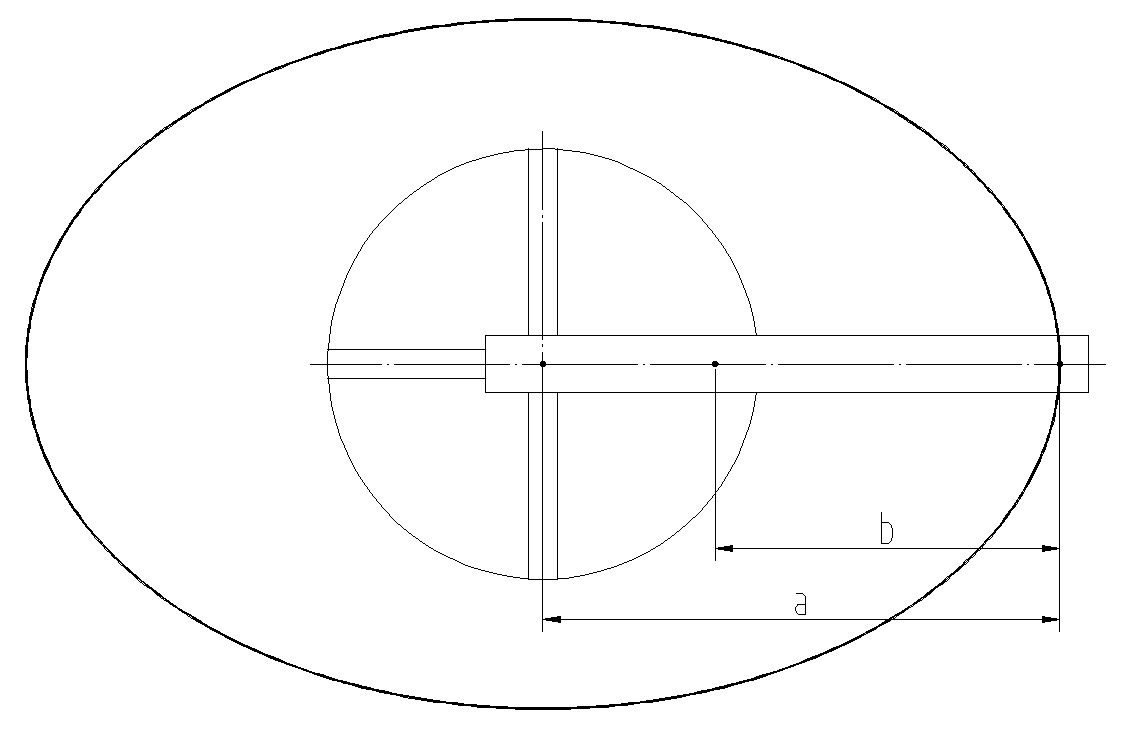
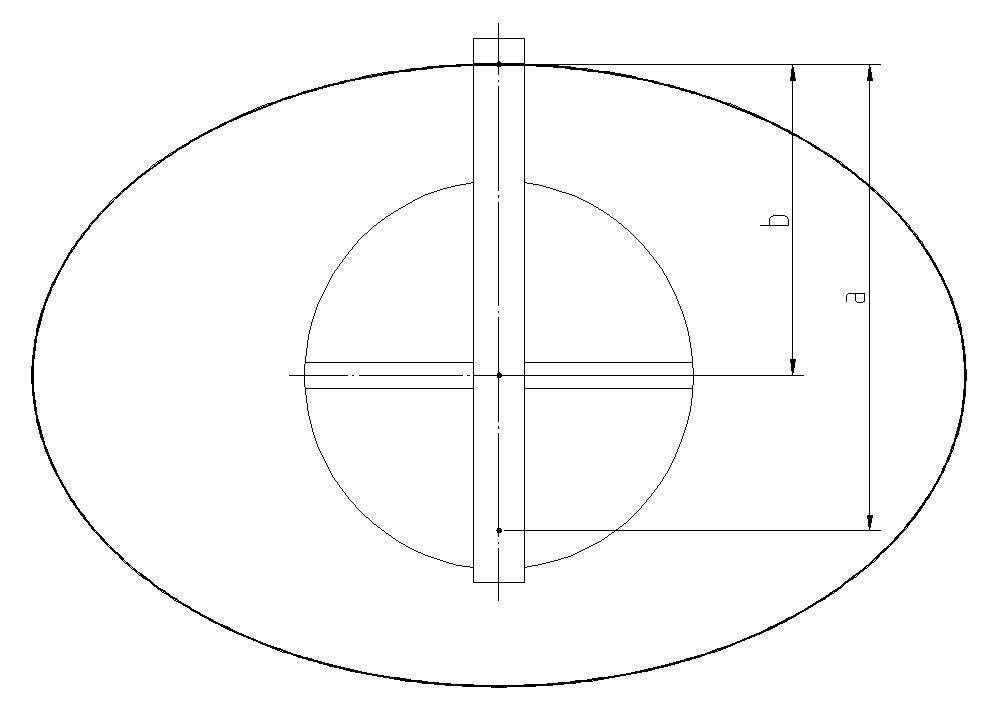
AP 長度為 a，BP 長度為 b，θ 為 BP 與水平線之夾角，以 O 為原點 $(0,0)$，則可知 P 點位置為 $(a\cos \theta ,b\sin \theta )$，$x=a\cos \theta$，$y=b\sin \theta$

$$\mathrm{因}\mathrm{為}{\sin }^2\theta +{\cos }^2\theta =1$$$$\mathrm{可}\mathrm{以}\mathrm{推}\mathrm{得}\mathrm{橢}\mathrm{圓}\mathrm{標}\mathrm{準}\mathrm{式}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

3D 列印成品

相關影片